数组是最常见最基础的数据结构了,由于它在内存中是顺序存储的,因此按下标查询的效率很高。
下面是一些我刷的数组题目的一些思路和代码。
思路
首先想到了可以利用暴力法直接遍历出所有的容器大小,时间复杂度为$O(n^2)$
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public int maxArea(int[] height) {
if (height.length == 0) {
return 0;
}
int maxArea = Integer.MIN_VALUE;
int head = 0;
int tail;
while (head < height.length - 1) {
tail = height.length - 1;
while (tail > head) {
int minSide = Math.min(height[head], height[tail]);
maxArea = Math.max(maxArea, (tail - head) * minSide);
tail --;
}
head ++;
}
return maxArea;
}
|
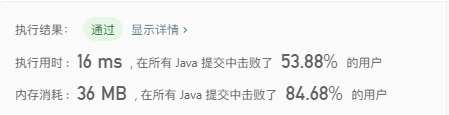
提交结果

时间复杂度过于高了,该怎么优化下呢?
最初我们考虑由最外围两条线段构成的区域。现在,为了使面积最大化,我们需要考虑更长的两条线段之间的区域。如果我们试图将指向较长线段的指针向内侧移动,矩形区域的面积将受限于较短的线段而不会获得任何增加。但是,在同样的条件下,移动指向较短线段的指针尽管造成了矩形宽度的减小,但却可能会有助于面积的增大。因为移动较短线段的指针会得到一条相对较长的线段,这可以克服由宽度减小而引起的面积减小。
优化后的代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| public int maxArea(int[] height) {
if (height.length == 0) {
return 0;
}
int maxArea = Integer.MIN_VALUE;
int head = 0;
int tail = height.length - 1;
while (head < height.length - 1) {
int minSide = Math.min(height[head], height[tail]);
maxArea = Math.max(maxArea, (tail - head) * minSide);
if (height[head] > height[tail]) {
tail --;
} else {
head ++;
}
}
return maxArea;
}
|
提交结果
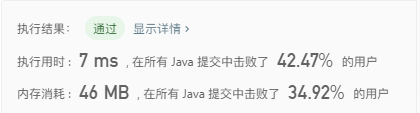
瞬间快了好多,美滋滋😎
思路
由于要计算三个数的和,如果用暴力法,会用$O(n^3)$的时间复杂度,对于这道题目会太慢了,那应该如何降低时间复杂度呢?
首先可以对数组进行排序,快速排序的时间复杂度是$O(nlogn)$,这个对速度的影响不是很大。
遍历nums数组,在使用双指针,第一个指针指向 l = i + 1 处,第二个指针指向末尾处,即 r = nums.length - 1处
再根据当前三个数字的和 thisSum = nums[l] + nums[r] + nums[i] 的结果,判断与目标 target 的距离,更新当前最近距离。
然后判断 thisSum 与 target 的大小关系,由于数组已经是有序的,若 thisSum > target 则 r--,若 thisSum < target 则 l++,否则说明已经找到 target ,直接返回结果即可
整个遍历过程的时间复杂度是$O(n^2)$,则总时间复杂度为 $O(nlogn) + O(n^2) = O(n^2)$
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| public int threeSumClosest(int[] nums, int target) {
if (nums.length < 3) {
return target;
}
Arrays.sort(nums);
int closetNum = nums[0] + nums[1] + nums[2];
for (int i = 0; i < nums.length - 2; i++) {
int l = i + 1;
int r = nums.length - 1;
while (l < r) {
int thisSum = nums[l] + nums[r] + nums[i];
if (Math.abs(thisSum - target) < Math.abs(closetNum - target)) {
closetNum = thisSum;
}
if (thisSum > target) {
r--;
} else if (thisSum < target) {
l++;
} else {
return thisSum;
}
}
}
return closetNum;
}
|
提交结果