LeetCode刷题：数组和链表

学习了那么多的数据结构和算法，到了检验学习成果的时刻了！！😎

关于数组和链表的几个必知必会的代码实现

数组

• 实现一个支持动态扩容的数组

• 实现一个大小固定的有序数组，支持动态增删改操作

• 实现两个有序数组合并为一个有序数组

链表

• 实现单链表、循环链表、双向链表，支持增删操作

• 实现单链表反转

• 实现两个有序的链表合并为一个有序链表

• 实现求链表的中间结点

数组题目

Three Sum（求三数之和）

题目：

给定一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？找出所有满足条件且不重复的三元组。

注意：答案中不可以包含重复的三元组。

例如, 给定数组 nums = [-1, 0, 1, 2, -1, -4]，

满足要求的三元组集合为：

[
  [-1, 0, 1],
  [-1, -1, 2]
]

思路：

最外层控制一个元素的循环，内层用双指针，一个从头到尾扫描，另一个从尾到头扫描，判断三个元素的值之和是否为零。

注意：相同的元素需要跳过

代码：

public List<List<Integer>> threeSum(int[] nums) {
    if (nums.length < 3) {
        return new ArrayList<>();
    }
    //排序
    Arrays.sort(nums);
    List<List<Integer>> result = new ArrayList<>();
    for (int i = 0; i < nums.length; i++) {
        if (nums[i] > 0) {
            break; // 如果当前数字大于0，则三数之和一定大于0，所以结束循环（没有0或负数怎么加也不会等于0）
        }
        if (i > 0 && nums[i] == nums[i - 1]) {
            continue; // 去重
        }
        int left = i + 1;
        int right = nums.length - 1;
        while (left < right) {
            int sum = nums[i] + nums[left] + nums[right];
            if(sum == 0){
                result.add(Arrays.asList(nums[i], nums[left], nums[right]));
                while (left < right && nums[left] == nums[left+1]) {
                    left++; // 去重
                }
                while (left < right && nums[right] == nums[right-1]) {
                    right--; // 去重
                }
                left++;
                right--;
            } else if (sum < 0) {
                left++;
            } else {
                right --;
            }
        }
    }
    return result;
}

Majority Element（求众数）

题目：

给定一个大小为 n 的数组，找到其中的众数。众数是指在数组中出现次数大于 ⌊ $\frac n 2$ ⌋ 的元素。

你可以假设数组是非空的，并且给定的数组总是存在众数。
示例 1:

输入: [3,2,3]
输出: 3
示例 2:

输入: [2,2,1,1,1,2,2]
输出: 2

思路：

根据题意，众数是指在数组中出现次数大于 ⌊ $\frac n 2$ ⌋ 的元素，因此可以先把数组排序，数组$\frac n 2$下标处就是众数。

代码：

public int majorityElement(int[] nums) {
    if (nums.length < 1) {
        return 0;
    }
    Arrays.sort(nums);
    return nums[nums.length/2];
}

然而你以为这样就完了吗？通过官方题解，还看到了一种更厉害的解法，那就是 Boyer-Moore 投票算法，思路如下：

如果我们把众数记为 $+1$ ，把其他数记为 $−1$ ，将它们全部加起来，显然和大于 0 ，从结果本身我们可以看出众数比其他数多。

本质上，Boyer-Moore 算法就是找 nums 的一个后缀 $suf$ ，其中 $suf[0]$ 就是后缀中的众数。我们维护一个计数器，如果遇到一个我们目前的候选众数，就将计数器加一，否则减一。只要计数器等于 0 > > ，我们就将 nums 中之前访问的数字全部忘记 ，并把下一个数字当做候选的众数。直观上这个算法不是特别明显为何是对的，我们先看下面这个例子（竖线用来划分每次计数器归零的情况）

[7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 7, 7, 7, 7]

首先，下标为 0 的 7 被当做众数的第一个候选。在下标为 5 处，计数器会变回 0。所以下标为 6 的 5 是下一个众数的候选者。由于这个例子中 7 是真正的众数，所以通过忽略掉前面的数字，我们忽略掉了同样多数目的众数和非众数。因此，7 仍然是剩下数字中的众数。

[7, 7, 5, 7, 5, 1 | 5, 7 | 5, 5, 7, 7 | 5, 5, 5, 5]

现在，众数是 5 （在计数器归零的时候我们把候选从 7 变成了 5）。此时，我们的候选者并不是真正的众数，但是我们在遗忘前面的数字的时候，要去掉相同数目的众数和非众数（如果遗忘更多的非众数，会导致计数器变成负数）。

因此，上面的过程说明了我们可以放心地遗忘前面的数字，并继续求解剩下数字中的众数。最后，总有一个后缀满足计数器是大于 0 的，此时这个后缀的众数就是整个数组的众数。

代码如下：

public int majorityElement(int[] nums) {
    int count = 0;
    Integer candidate = null;

    for (int num : nums) {
        if (count == 0) {
            candidate = num;
        }
        count += (num == candidate) ? 1 : -1;
    }

    return candidate;
}

Missing Positive（求缺失的第一个正数）

题目：

给定一个未排序的整数数组，找出其中没有出现的最小的正整数。

示例 1:

输入: [1,2,0]
输出: 3

示例 2:

输入: [7,8,9,11,12]
输出: 1

说明:

你的算法的时间复杂度应为$O(n)$，并且只能使用常数级别的空间。

思路：看到说明后就知道不能用哈希表来解决了，所以要换个思路，想了半天想不明白，咱也不敢说，咱也不敢问，只好去偷瞄一眼官方题解，看了后才觉得还是大佬们🐂🏆。点击此处链接

代码如下：

public int firstMissingPositive(int[] nums) {
  int n = nums.length;

  // 基本情况
  int contains = 0;
  for (int i = 0; i < n; i++)
    if (nums[i] == 1) {
      contains++;
      break;
    }

  if (contains == 0)
    return 1;

  // nums = [1]
  if (n == 1)
    return 2;

  // 用 1 替换负数，0，
  // 和大于 n 的数
  // 在转换以后，nums 只会包含
  // 正数
  for (int i = 0; i < n; i++)
    if ((nums[i] <= 0) || (nums[i] > n))
      nums[i] = 1;

  // 使用索引和数字符号作为检查器
  // 例如，如果 nums[1] 是负数表示在数组中出现了数字 `1`
  // 如果 nums[2] 是正数 表示数字 2 没有出现
  for (int i = 0; i < n; i++) {
    int a = Math.abs(nums[i]);
    // 如果发现了一个数字 a - 改变第 a 个元素的符号
    // 注意重复元素只需操作一次
    if (a == n)
      nums[0] = - Math.abs(nums[0]);
    else
      nums[a] = - Math.abs(nums[a]);
  }

  // 现在第一个正数的下标
  // 就是第一个缺失的数
  for (int i = 1; i < n; i++) {
    if (nums[i] > 0)
      return i;
  }

  if (nums[0] > 0)
    return n;

  return n + 1;
}

链表题目

Linked List Cycle I（环形链表）

题目：

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。 如果 pos 是 -1，则在该链表中没有环。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

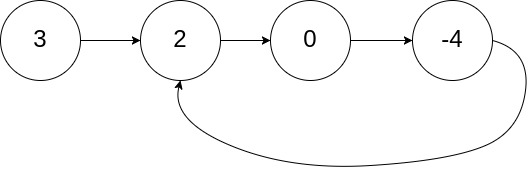
思路：此题即是单向链表的常见操作中链表环的检测，可以直接点击点链接跳转去看看。

这里直接给出代码：

public boolean hasCycle(ListNode head) {
    if (head == null || head.next == null) {
        return false;
    }
    ListNode slow = head;
    ListNode fast = head.next;
    while (slow != fast) {
        if (fast == null || fast.next == null) {
            return false;
        }
        slow = slow.next;
        fast = fast.next.next;
    }
    return true;
}

Merge k Sorted Lists（合并 k 个排序链表）

题目：

合并 k 个排序链表，返回合并后的排序链表。请分析和描述算法的复杂度。

示例:

输入:

[
  1->4->5,
  1->3->4,
  2->6
]

输出: 1->1->2->3->4->4->5->6

思路：这里直接给出官方题解的链接，因为有很多种方法可以解决这个问题，详见官方题解

代码如下：这里给出利用优先队列实现的代码

public ListNode mergeKLists(ListNode[] lists) {
    PriorityQueue<ListNode> queue = new PriorityQueue<>(Comparator.comparingInt(node -> node.val));
    ListNode dummy = new ListNode(0);
    ListNode p = dummy;
    queue.addAll(Stream.of(lists).filter(Objects::nonNull).collect(Collectors.toList()));
    while (!queue.isEmpty()) {
        ListNode node = queue.poll();
        p.next = node;
        p = p.next;
        if (node.next != null)
            queue.add(node.next);
    }
    return dummy.next;
}

做完题目之后，你可以点击左侧的分享，把测试题分享给你的朋友，说不定就帮他解决了一个难题。也可以给我留言，和我一起分享。